Enhetsvektor notasjon | Vektorer og mellomrom | Lineær algebra | Khan Academy
Når de forklarer Dimensjon W, blir den representert som den negative siden av X-aksen. Hvorfor er dimensjon W negativ X? Er det ikke egentlig dens egen dimensjon?

- Prøv å tegne en 4-dimensjonal graf på en 2-dimensjonal overflate. Dette er hva de kom på (din rett, selv om det ikke er en flott graf).
Som @NendoTaka har nevnt, er det ganske vanskelig å tegne et 4d-objekt på en 2d-overflate.
Slik fungerer dimensjonalitet:
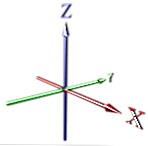
med en enkelt dimensjon sendes et punkt uendelig, og skaper en linje (se X)
i 2d legger vi til en dimensjon vinkelrett på den (se X, Y).
Deretter går vi vinkelrett igjen og utvider oss oppover for å få den tredje dimensjonen (se X, Y, Z).
Fordi 3d> 2d, kan vi ikke representere det godt på papir uten å brette papiret eller legge til flere ark på toppen av det - alt veldig upraktisk for visning på en skjerm. Så i stedet bruker vi perspektiv - hvordan øynene våre oppfatter 3d. Vanligvis er vinklene her ~ 30 grader.

Og det ser ganske greit ut, for øynene våre ser ikke i denne tradisjonelle 3d-forstanden, så etterligning som fungerer. Men når vi vil representere en fjerde dimensjon, har vi ikke noe å sammenligne det med. Vi må gå vinkelrett igjen, og dette er vanskelig for våre øyne å forstå, siden vi ikke har så mye referanse.
Her er et eksempel på en fjerde dimensjon:
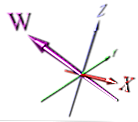
Dette er en mer korrekt måte å vise dimensjonen på, men den er fortsatt avhengig av perspektiv - det er heller ikke umiddelbart åpenbart at det er en ny dimensjon ved første øyekast.
Animatørene valgte sannsynligvis å gjøre noe enkelt som det ville være lettere å animere. Selv om X og W-dimensjonene roteres over bildet ovenfor, kan det overlappe hverandre - og dette ville ikke være tydelig i bildet uten pekepekere.
Så ja, de tar feil - men det er heller ikke en enkel måte å representere fire dimensjoner på et enkelt papirark
Koordinere bildekilder og les godt
3- 1 For å være rettferdig er det mange standard måter å projisere 4-dimensjonale objekter som tesserakter og 3-sfærer i 3 dimensjoner (og deretter ned til 2 dimensjoner på vanlig måte) som er langt bedre enn den som ble brukt i showet, mange hvorav har den ekstra bonusen å se kulere ut enn den som ble brukt i showet.
- @senshin oh for sure, men jeg antar at animatørene også ønsket å forklare noe, i stedet for å forbløffe
- 1 Du kan bruke andre ting enn posisjon for å indikere hvor langt langs en akse noe er, som farge.







